At this point I cannot avoid mentioning what I would undoubtedly consider the “king” of all introductory animation courses, the Bouncing Ball.

Obviously I will talk about it in more detail in a next chapter, but for now I’ll just try to make you understand why this apparently stupid and very elementary exercise is in my opinion so important and fundamental in the context of a general “vision” of our art.

It is, as you will have already guessed at this point, an ideal “development” of Albert Michotte’s perceptive experiments which I have already introduced previously in this same chapter (12 – Casuality and Causality).

Although they are two completely distinct approaches, also because they are defined in very distant disciplinary fields, they ideally make up a perfectly coherent discussion for the purposes we have set ourselves.

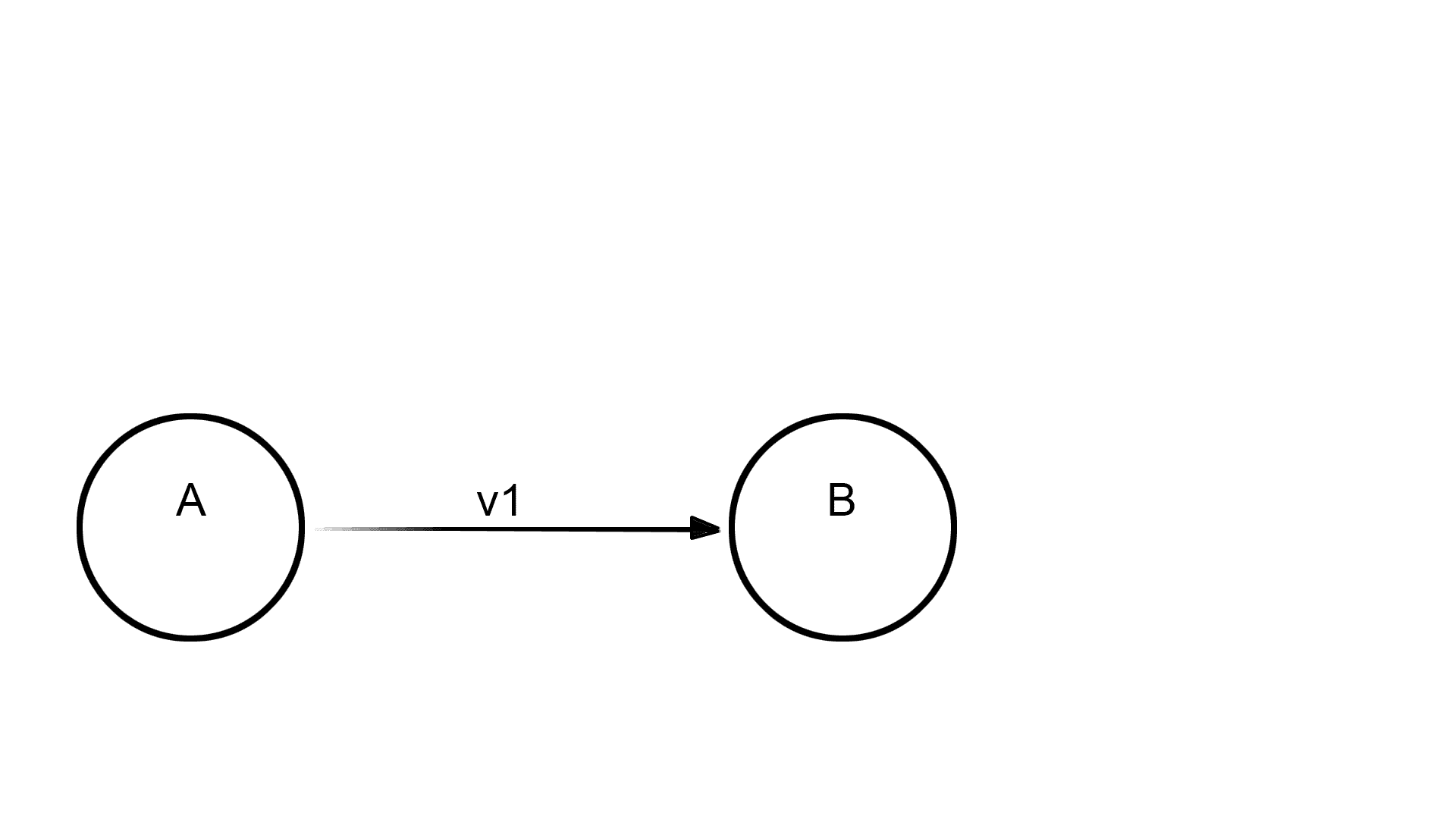
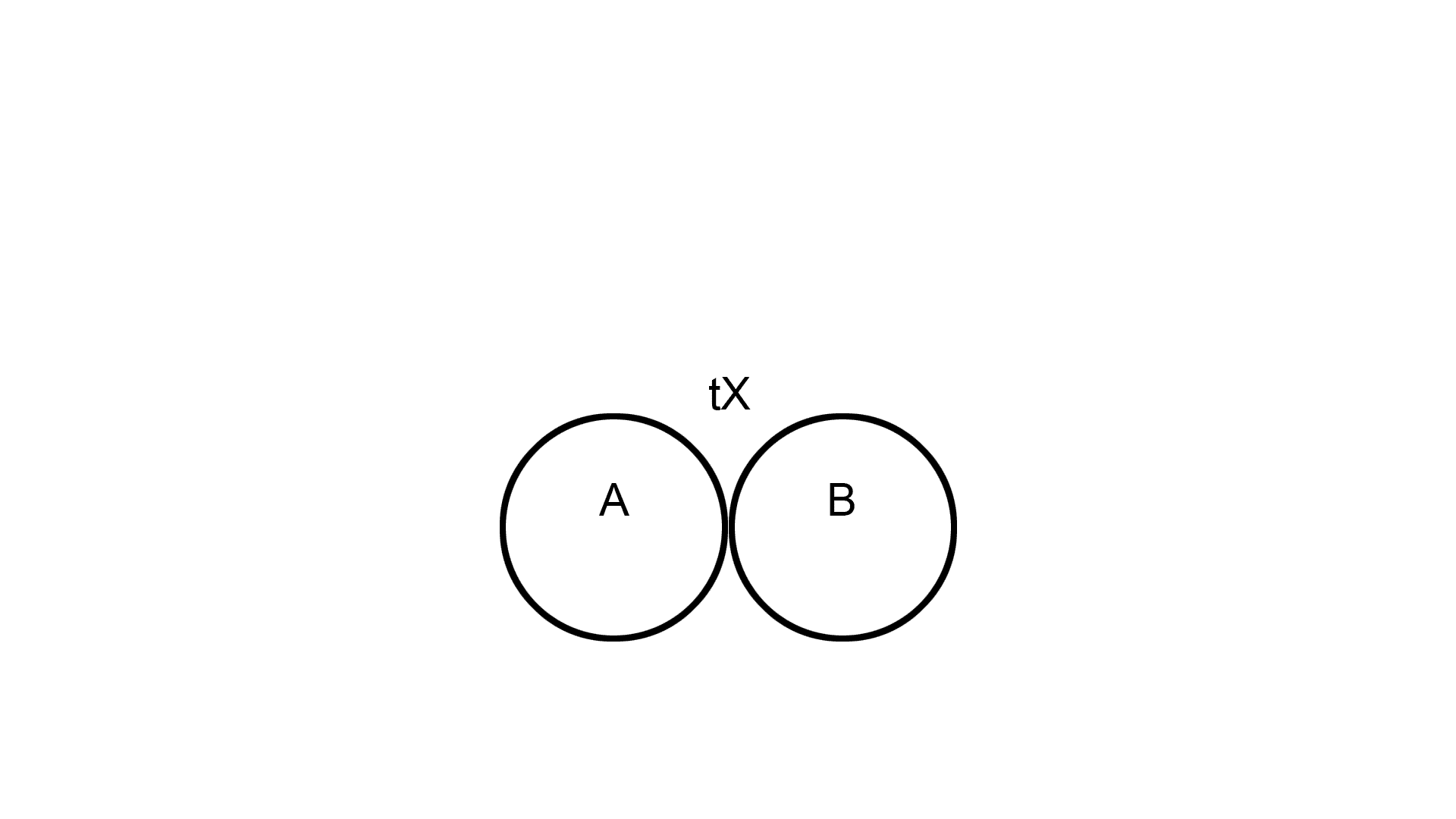
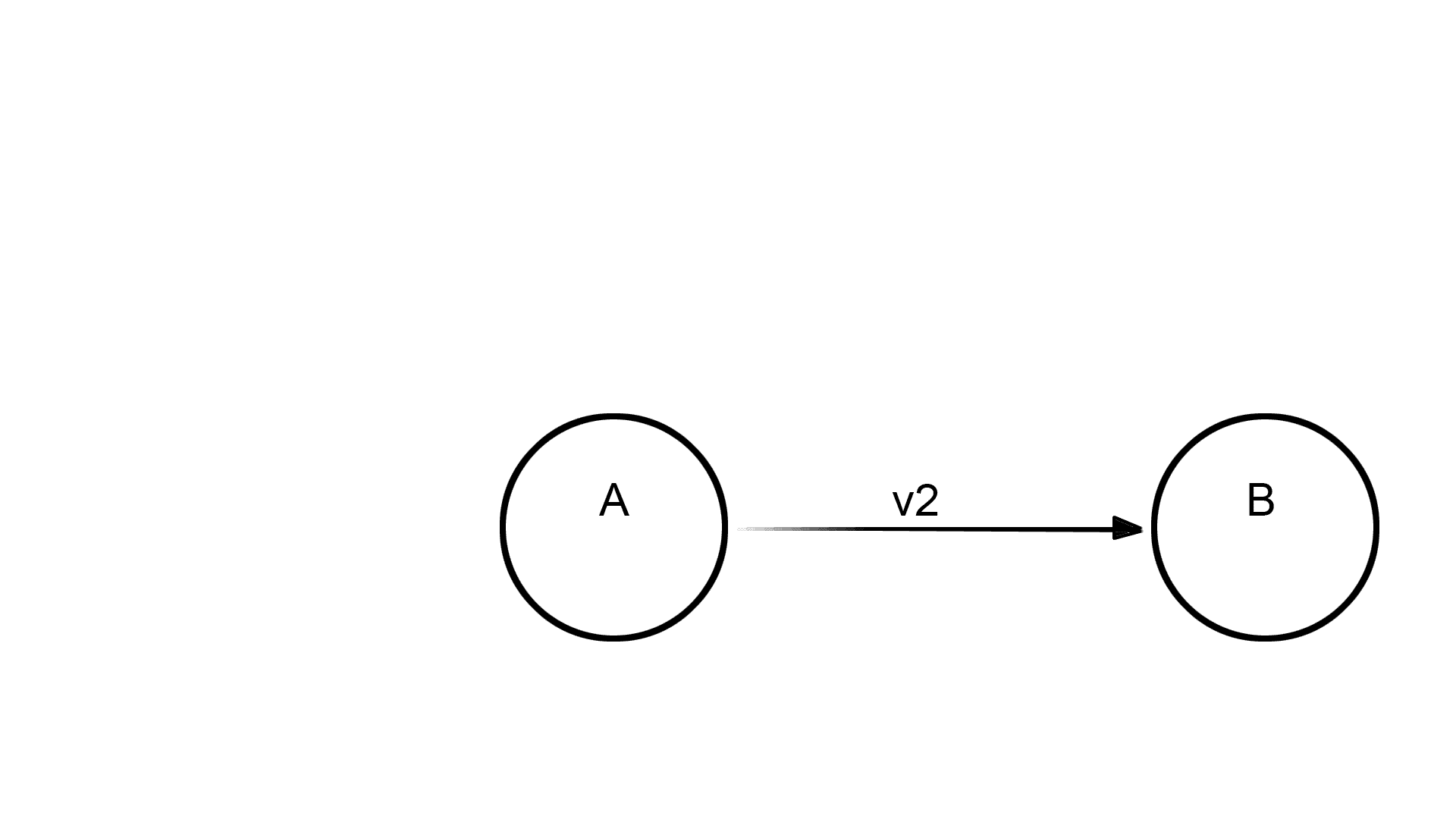
Returning to Michotte’s causality experiments, we have seen that by appropriately varying the parameters of relative speed and contact time between two abstract and two-dimensional objects we can obtain very different trigging and launching effects.

In the “classic” example, an object [A] moves at a speed [v1] (Fig 15.01), meets an object [B] with a contact time between the two of [tX] – in this case 1/ 25 of a second or 40 milliseconds, equal to 1 PAL video equivalent frame – and stops (Fig 15.02), while the object [B] starts in the same apparent direction at a speed [v2], in this case about the half that of [A] (Fig 15.03). The perception you get is that object [A] CAUSES the object [B]consequent movement (Vid15.01).

As you see, this is an entirely virtual event, as the two objects are not real, they don’t have mass, volume or material. Moreover their movement is obtained cinematically – and therefore it is not continuous, but sampled, at 1/25 of a second – and it is completely inferred by our perceptual system.

We can now vary a single parameter, such as the contact time between the two objects [tX], bringing it to 240 milliseconds (equivalent to six frames at 25 FpS), and thus the effect is canceled: the two movements of [A ] and [B] are only chronologically subsequent, but independent of each other. No causal effect is anymore perceived (Vid15.02).

If, however, we try to modify the speed ratio between the two objects, inverting them, i.e. the object [B]moves at a higher speed than that of the object [A], we will obtain the curious (if predictable) effect of an “ESCAPE” of the object [B] from the object [A] (Vid15.03), obtaining, in addition to the pure effect of “causality”, also an, albeit primitive, effect of “intentionality”, at least on the part of this last item. Until now the two movements were both in a certain way “passive”, at this point instead the object [B] seems to actively “escape” from the other, and therefore express its own intention – and also emotion, such as “fear” ” or “disgust” – in performing this action.

Up to now the movements (i.e. speeds) in play were constant (linear), but here’s what happens when we add a new parameter, that of ACCELERATION.

Here the object [A] reaches the object [B] at a linear speed. At the moment of contact, instead of stopping instantly on the spot, it continues its path for a short distance, gradually decelerating until it stops. At the same time, the object [B] sets off in the same direction at a speed initially only slightly lower, or even equal, to that of the other object at the moment of impact, gradually decelerating until it stops at a certain distance from the first object. (Vid15.04)

Here the effect of “intentional causality” is not only accentuated, but we begin to perceive the nature of the two objects in the field: not all the energy is transferred from object [A] to object [B], but a part of it is dynamically dissipated by the first object itself, giving a primitive perceptive indication of the relative mass and constituent material of the two objects.

If the object [A] then enters the field at a certain speed and gradually decelerates until it stops in contact to the object [B], and only after a certain time [tX], which can even reach a significant value, the object [B]moves away from object [A] by ACCELERATING, then the “intentional escape” effect will be further strengthened, and at this point we will probably be able to deduce a certain intentionality (threat, hostility) also in the approaching action by the object [A] to [B] (Vid15.05).

Finally, if we coherently combine the processing of all these parameters (speed, contact time, acceleration/deceleration), we can obtain an even more significant and elaborated effect, in which we can clearly “see” the object [A] approaching “threateningly” the object [B], who, after a moment’s hesitation, quickly moves away due to his own reaction (fright, surprise, hostility) from the object [A] (Vid15.06).

We could even completely cancel the contact time, or even make it “negative”, so that the object [B] moves BEFORE the arrival of the object [A] in its vicinity: the “escape” effect would be further accentuated by a greater sense of intentionality (Vid15.07). But here we are already in an area that we could define as a real, albeit elementary, character animation.

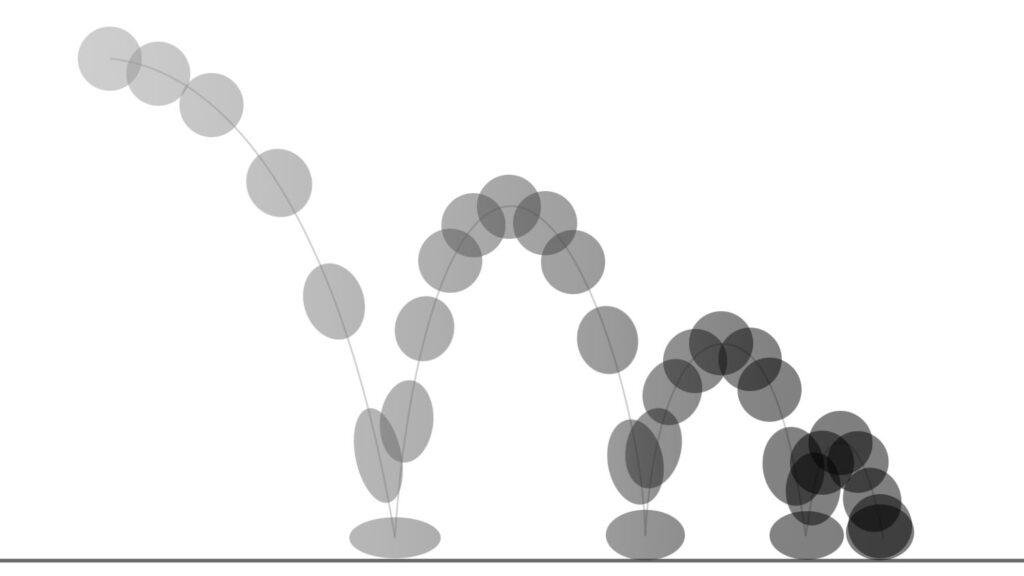
The traditional “bouncing ball exercise” that we will now briefly talk about, if we think about it, compared to Michotte’s scenario simply replaces one of the two objects on the field, object [B], with a totally “passive” and static one (although we will see that it too can in turn be in some way “animated”) which – conventionally – we define as “GROUND”, but which could be any other “fixed” ideal object against which the object [A], or conventionally our ” Ball”, exercises its action: it could be a “wall” or a vertical barrier, if the movement develops in a horizontal line, or even any other stationary object, even a second Ball, as long as it is fixed compared to the first.

So here it is only the object [A] that performs the action, and this involves both a simplification and an enrichment of the perceptual effect.

In the classic version of this famous (and infamous) exercise (Vid15.08), the “Bouncing Ball” makes use, as in Michotte’s scenarios, of three main parameters: Speed in[v1– in Acceleration] (Fig 15.04) in entry, or fall, Time [tX] (Fig 15.05) of contact with the Ground, and Speed out [v2 – in Deceleration] (Fig 15.06) in exit, or rebound.

By varying these parameters we can obtain different perceptual effects, fundamentally linked to the “physical” quality of the objects (the Ball and the Ground) in play. Here we are no longer dealing with “causality” (and therefore intentionality), but with the “concreteness” of the objects, that is, their mass, or weight, their greater or lesser “solidity”, and the nature of the material of which they are made.

Here too I limit myself to just a few crucial examples.

We know well that by modifying some of the parameters we can obtain different but vivid perceptions primary of the “weight” inherent to the object. And even in this case these are effects inferred by the observer’s perceptive system alone, as the objects in play are totally abstract representations: they “really” have no mass or weight, no concreteness, no three-dimensionality or material, they are a pure representation of an event.

By varying the motion parameters alone, we can make an object convey its greater or lesser weight (mass), such as light as a balloon (Vid15.09) or as heavy as a leather ball (Vid15.10) or heavy as a boulder (Vid15.11).

By acting instead on the contact time of the object with the ground, we can obtain the illusion of a voluntary action on the part of the object: the ball, once on the ground, ideally picks up momentum and makes a voluntary leap, no longer just rebounding (Vid15.12); up to obtain, when the contact time exceeds a certain threshold, the cancellation of the effect itself, two separate outward and return movements, with no longer any cause or effect relationship between them (Vid15.13).

But at this point a completely new and original element appears in the mechanics of the bouncing ball: the Squash & Stretch effect.

This is an effect unique to animation, and Albert Michotte would certainly have considered it spurious, extraneous to the object of his research. For us, however, it represents a fundamental turning point, the one in which the object is charged with its own, vital energy, in itself and not just in relation to another object, as was the case for example in the “escape” effect of the “causality” experimental set illustrated above. It is no longer a “cause and effect” phenomenon, but an internal impulse within the object itself. The object becomes fully “the subject” (or “the actor”) of an action.

In the classic example (Vid15.14) the sole presence of the Squash & Stretch effect is limited to making the movement more “fluid and natural” to the observer’s eye, but it is enough to modify a couple of parameters (Contact Time and Acceleration – Vid15.15) and the event takes on a whole new meaning. It is no longer a more or less passive “bounce”, but it is the ball itself that dampens the impact of the fall, gains momentum, and voluntarily jumps away.

Squash & Stretch are still two completely arbitrary parameters here, as they have no direct basis in objective reality. If we test a sequence shot from life (Fig15.16), for example, we can actually “see” the Stretch as motion blur, which is in any case an artefact due to the sampling of the movement from a shutter at 25 fps, while we practically do not see any visible trace of the Squash.
Actually, a “squashing” effect of a real elastic ball is physically present, but to an almost imperceptible extent, which brings us to another of the primary “principles” of classical animation, as we will see later: the exaggeration (Fig15.17).

Finally, if we simply eliminate the “entry” movement and keep all the other parameters intact (Vid15.18), we will get a true minimal animation of an object gaining momentum and voluntarily making a leap upwards.

The object, which up to this point the movement transformed into the subject of an action, thus fully becomes an “Actor”.

But at this point we are about to meet another famous funny and silly guy: the flour sack.

16 – Acting and Feeling (Part I)